The National Institute of Standards and Technology (NIST) has selected four encryption tools in July 2022 to withstand a future quantum computer’s assault, which might break the privacy protection in digital systems we rely on every day, such as online banking and email software. The post-quantum cryptographic standard, which will be finalized in about two years, will include four algorithms. Three of them use the Lattice method.
How current asymmetric cryptography works ?
Users can encrypt information using asymmetric encryption (also known as asymmetric cryptography). To ensure that only the intended recipient can see what you’ve written, you want to send it over the internet. Asymmetric cryptography can help you accomplish that. Asymmetric cryptography allows for extremely secure communication between two parties. Even if you’ve never heard of it before, you’ve probably encountered this technology. Websites with addresses beginning with “https” use this technology, for example. This is also the type of cryptography used by ransomware.
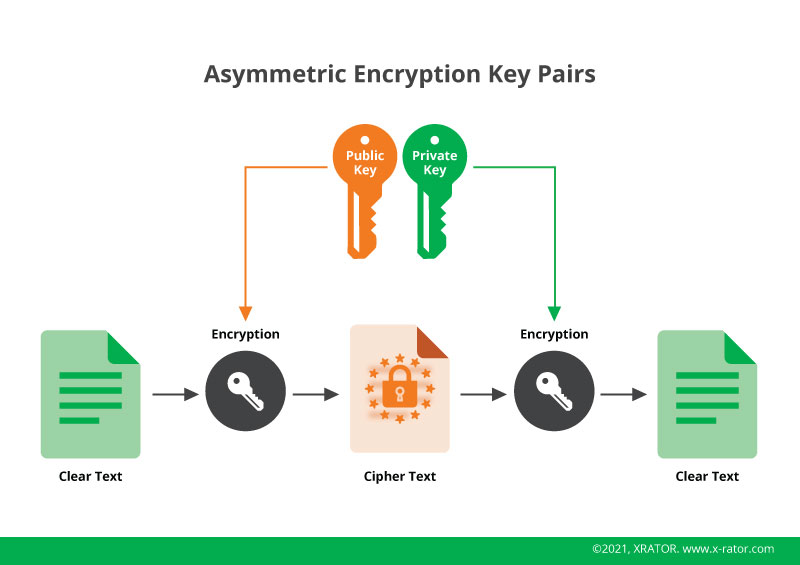
An asymmetric encryption environment provides two keys to ensure security:
- Public-key: a shared key used to make a message only readable by the holder of the Private Key
- Private-key: a key that has to be kept secure and attribute to a single machine, person or organization.
Asymmetric cryptography improves the security of the symmetric cryptography, which only use one key. The problem was then how to transmit this single key with no possibility for a malicious person to intercept it and decrypt the communication.
Why quantum computing is a risk to asymmetric cryptography ?
Security experts now well recognize the risk posed by quantum computing to modern cryptography. Shor’s quantum algorithm, in particular, provides attackers with a large theoretical speedup for brute-forcing cryptosystems such as RSA and ECDSA that rely on public keys.
What Shor revealed in his 1994 algorithm was that a quirk of factoring makes it vulnerable to attack by quantum computers. It is a very specific in which quantum computer excel. So after Shor, cryptographers had a new job: Find a novel set of mathematical operations that are easy to do but nearly impossible to undo.
Quantum computing has already begun to offer insight into how vulnerable conventional encryption is to quantum computers. Enough physical qubits might break all of these cryptosystems in a few hours. Lattice cryptography has been one of the most successful counter measure so far. It relies on the difficulty of reverse-engineering sums of points, which was first developed in the 1990s.
How does Lattice method works ?
Lattice multiplication, also called Chinese multiplication, is a written approach for multiplying numbers. People normally use it to solve problems involving multi-digit multiplication. A visual representation of the steps involved in multiplication can help students better understand the process and avoid making mistakes. This method also helps students ensure that the numbers are properly aligned by providing a model.
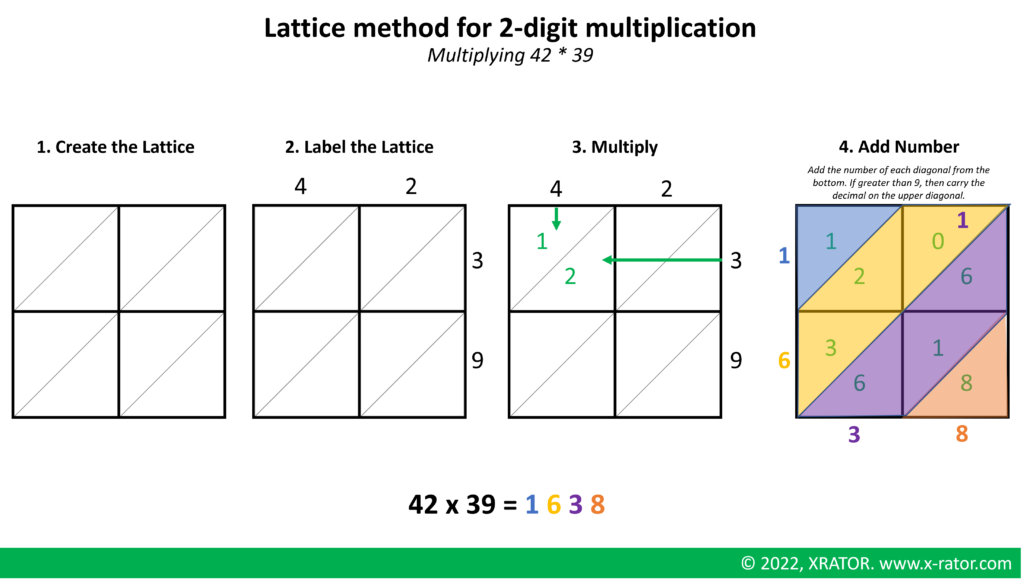
When working with larger numbers, you can follow the same 4 steps. We just would draw the lattice larger. For example, if you were multiplying a 3-digit number by a 4-digit number, you would need to draw a 3×4 grid. Make sure the grid matches the number of digits.
Lattice algorithm applied to cryptography
Researchers have extensively studied and understood lattices as hard maths problems. Mathematicians have been studying lattices since at least the early 1800s, when Johann Gauss discussed them. Lattice problems are proving to be extremely flexible in enabling us to construct a wide range of cryptographic schemes.
In fact, we are able to replace essentially all of the cryptosystems currently at risk, as well as create new, powerful cryptographic tools of unknown type. Furthermore, we are able to produce quantum computers that cannot factor numbers or solve other hard mathematical problems. These include the families of hard problems that we believe will remain unresolved for the foreseeable future.
Lattice-based problems possess a technical property that cryptographers favour for cryptography based on lattices. In lattice-based crypto issues, we often only require the worst-case hardness of problems to verify the security of our protocols, rather than their typical-case hardness. Miklós Ajtai initiated lattice-based cryptography in 1996 based on this notion.
We will simplify the description of Lattice cryptography below. First we have to create the public key that Alice will be able to send to Bob, so that Bob can encrypts its message for Alice.
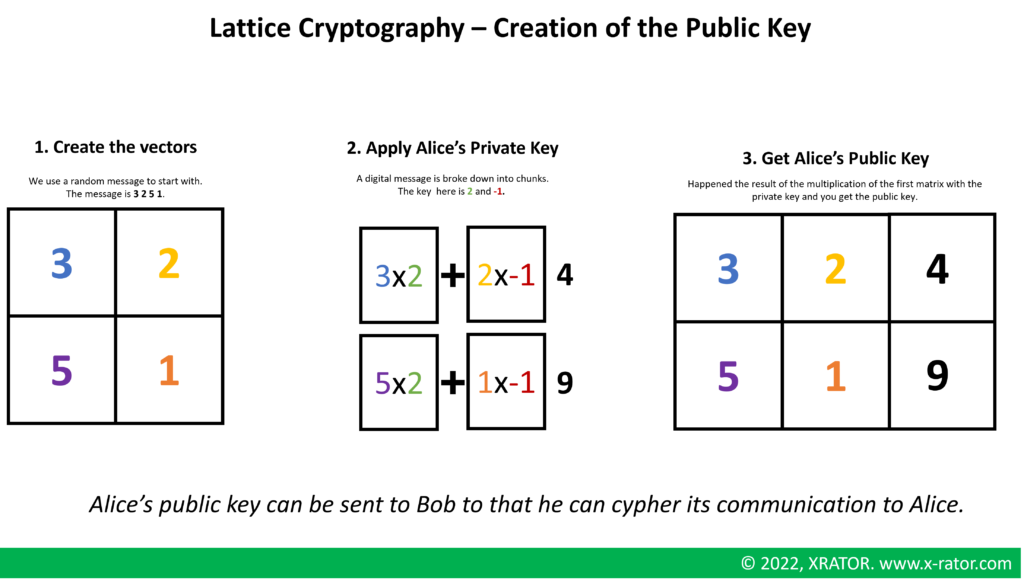
Bob can now use Alice’s public key to cypher his message. Alice can check that this matrix is not readable by an unauthorized party and that an attacker cannot change without her noticing it.
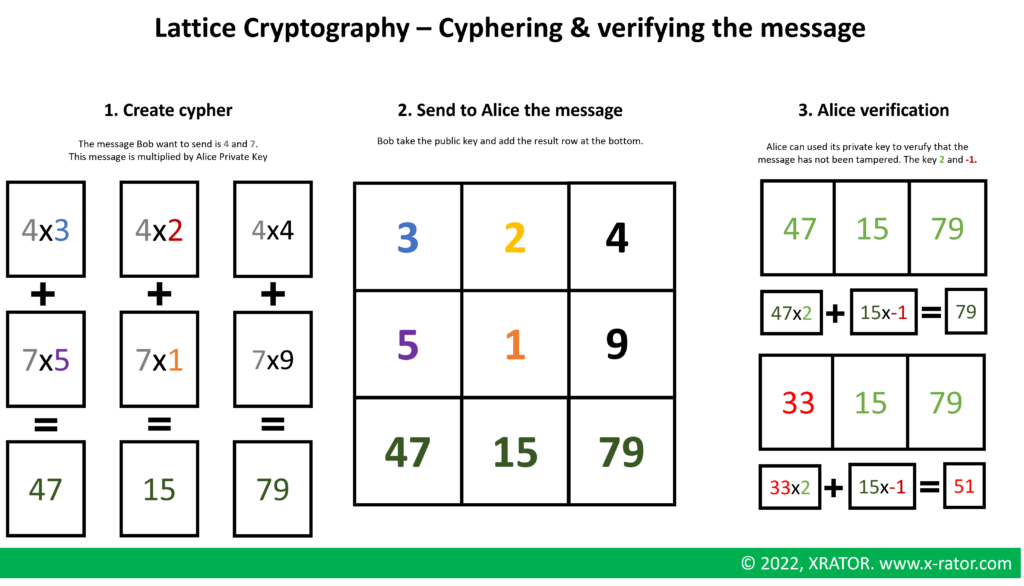
In practice, we use longer message. When people wishing to receive, for example, a 100-bit message will generate 100 new columns instead of just one. The sender then creates a new row by modifying the last 100 entries so that they either encode a 0 or a 1 for each entry.
Conclusion
We don’t know of any efficient quantum solution to these problems, making lattice cryptography quantum-resistant. Logically, computational complexity theorists rarely prove what cannot be done. However, if such proofs were possible, they would have widespread implications, such as the proof that P=NP.
Lattice based cryptography is quantum resistant because nobody knows how to break it using a quantum computer. Some argue that this method will be vulnerable to quantum attack too once an algorithm is developed for it. For example, solving the Hidden Subgroup Problem for dihedral groups would break many lattice-based cryptos.


